| Eignung der Korrelationsmatrix Bevor mit der eigentlichen Faktorenanalyse gestartet werden kann, sollte die Korrelationsmatrix auf ihre Eignung geprüft
werden.
Insbesondere wenn, wie in der Tabelle 4(5) dargestellt, Koeffizienten um 0,7 und 0,8 berechnet wurden. Es sei hier, wenn derartige Ergebnisse vorliegen, noch einmal auf eine Verteilungsprüfung hingewiesen.
Zur Prüfung, ob ein statistisch gesicherter Zusammenhang zwischen den Merkmalen M1 und M2 besteht, kann der t-Test der Korrelationskoeffizienten herangezogen werden. Wenn Sie die Prüfung durchgeführt haben, werden Sie feststellen, dass mit P=95% der Koeffizent 0,7 darauf hinweist, dass kein gesicherter Zusammenhang besteht. Prüfen Sie noch den Koeffizienten 0,8 für die Merkmale M2 und M3 ebenfalls mit P=95%, werden Sie ein grenzwertiges Ergebnis erhalten. Für dieses Beispiel wird aber weiterhin obige Matrix (Tabelle 4) verwendet.
Ein weiterer Test zur Eignung der Merkmale zur Faktorenanalyse ist der Bartlett-Sphärentest, dessen Prüfgröße v nach berechnet wird. Die Prüfgröße v folgt bei Normalverteilung einer Chi-Quadrat-Verteilung mit einem Freiheitsgrad f = m(m-1)/2. Es kann die Hypothese aufgestellt werden, dass eine Faktorenanalyse sinnvoll ist, wenn die Prüfgröße v > 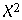 f,P ist f,P ist
Für das obige Beispiel nimmt die Prüfgröße v folgenden Wert an: v = -(6-1-(2*5+5)/6 * ln(0,00021214) = 21,146 f = m(m-1)/2 = 5(5-1)/2 = 10 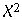 f=10,P=95%= 18,31 (Tabellenvergleichswert) f=10,P=95%= 18,31 (Tabellenvergleichswert)
v (21,146) > 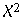 (18,31) (18,31)
Da die Prüfgröße v größer ist als der Chi-Quadrat-Vergleichswert, können die Merkmale zur Faktorenanalyse herangezogen werden. Die folgenden Methoden zur Eignungsprüfung werden nur noch kurz beschrieben, da sie von verschiedenen statistischen Programmen angeboten werden: - Inverse Korrelationsmatrix
Hier wird von der Eignung zur Faktorenanalyse ausgegangen, wenn die Inverse der Korrelationsmatrix eine Diagonalmatrix darstellt. D. h., die Elemente der inversen Matrix die nicht auf der Diagonalen liegen, sollen möglichst nahe bei Null liegen. Da es kein allgemein
gültiges Kriterium dafür gibt, wie weit diese Elemente von Null abweichen dürfen, ist die Entscheidung, ob die Korrelationsmatrix geeignet ist oder nicht, nicht sehr gesichert. - Anti-Image-Kovarianz-Matrix
Hier wird davon ausgegangen, dass die Varianz einer Variablen in zwei Teile zerlegbar ist, das Image und das Anti-Imgae. Unter Image wird der Teil der Varianz verstanden, der über
eine multiplen Regressionanalyse erklärt werden kann und der Anti-Image-Teil von den übrigen Variablen unabhängig, also nicht erklärbar ist. Die Variablen sind dann für eine Faktorenanalyse geeignet, wenn der Anti-Image-Teil möglichst gering ausfällt. Auch hier bedeutet dies, dass die Elemente der Anti-Image-Kovarianz-Matrix die nicht auf die Diagonale fallen, möglichst nahe bei Null liegen müssen.
Ebenso gilt hier der Hinweis,wie bei der inversen Korrelationsmatrix, der nicht sehr
gesicherte Entscheidung . Als Empfehlung kann herangezogen werden, dass die Elemente der Diagonalen absolut mind. 75 % gegenüber den nicht auf der Diagonalen liegenden Elementen ausmachen müssen. - Kaiser-Meyer-Olkin-Kriterium (KMO-Kriterium)
Auf Basis der Anti-ImageKovarianz-Matrix wurde durch Kaiser, Meyer und Olkin eine Prüfgröße, die als mesaure of sampling adequacy (MSA) bezeichnet wird, entwickelt.
Diese Prüfgröße MSA zeigt an, in welchem Ausmaß die Variablen zusammengehören und dient als Hinweis, ob eine Faktorenanalyse sinnvoll ist. Der Wertebereich der Prüfgröße MSA liegt zwischen 0 und 1 und folgende Beurteilung wird vorgeschlagen (Tabelle 6):
MSA-Wert | Bewertung | >= 0,9 | marvelous | >= 0,8
| meritorious | >= 0,7 | middling | >= 0,6 | mediocre | >= 0,5 | miserable | < 0,5 | unacceptable |
Tabelle 6 |
|
Eine Korrelationsmatrix mit einem MSA < 0,5 wird als nicht geeignet zur Faktorenanalyse angesehen. Wünschenswert ist ist ein MSA-Wert von >= 0,8.
In der Literatur wird der MSA-Wert als ein wichtiges Kriterium bezeichnet und ggf. durch Ihr Faktorenanalyseprogramm berechnet und angeboten. Wie immer, liegt die Beurteilung der MSA-Größe bei Ihnen.
Extraktion der Faktoren, mathematische Basis Nach dem die Korrelationsmatrix R auf ihre Eignung geprüft wurde und wir zur Faktorenanalyse mit dem Statistikprogramm R kommen, sollte die mathematische Basis als Übersicht dargestellt werden.
Dazu wird von der Annahme ausgegangen, dass jedes Element der Tabelle 2 oder der Z-Matrix (Tabelle 3) sich als Linearkombination der hypothetisch vorhandenen Faktoren darstellen lässt. Weiter oben wurde zur Berechnung des Korrelationskoeffizienten zum Aufbau der Korrelationsmatrix R durch den Verweis auf die entsprechende Seite als Möglichkeit dargelegt. Die Korrelationsmatrix R lässt sich auch wie folgt berechnen: |