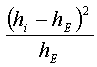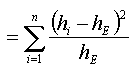![]() -Test, Chi2-Test, Chiquadrat-Test
-Test, Chi2-Test, Chiquadrat-Test
Der ![]() -Test ist ein Anpassungstest. Mit ihm lässt sich prüfen, ob die beobachtete Verteilung einer vorgegebenen Verteilung entspricht.
-Test ist ein Anpassungstest. Mit ihm lässt sich prüfen, ob die beobachtete Verteilung einer vorgegebenen Verteilung entspricht.
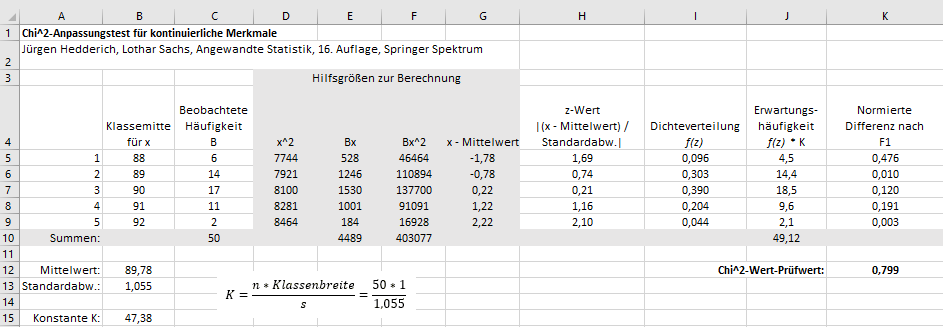
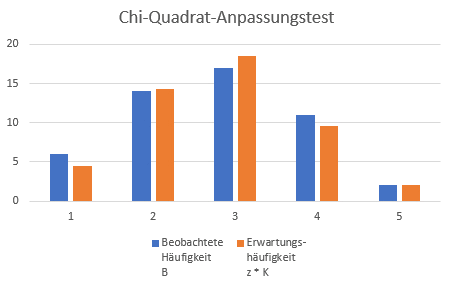
Dieser Test ist anwendbar für kategoriale oder auch für kontinuierliche Merkmale die klassifiziert wurden.
Kategoriale Merkmale
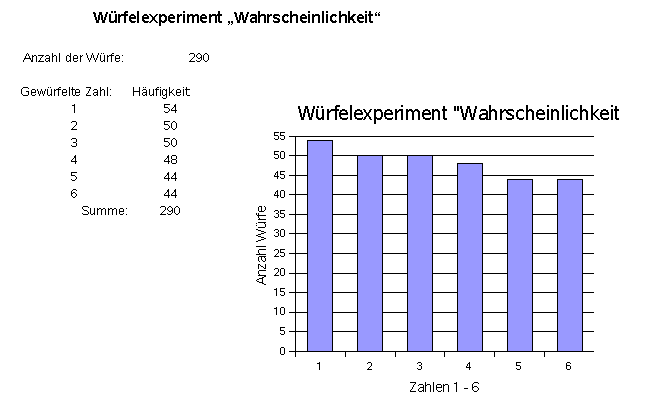
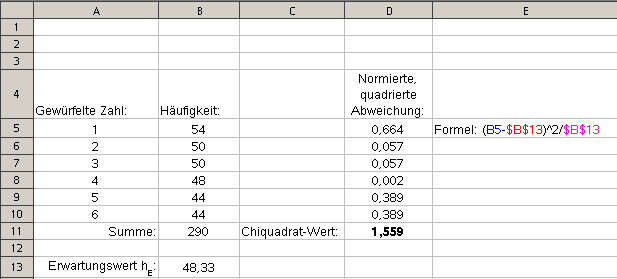
Hinweis: Schauen Sie zu diesem Würfel-Beispiel auch das Video Chi2 Anpassungstest auf YouTube!
Zur Darlegung des ![]() -Tests für kategoriale Merkmale gehen wir von diesem kleinen Würfelexperiment aus (Bild 1):
-Tests für kategoriale Merkmale gehen wir von diesem kleinen Würfelexperiment aus (Bild 1):