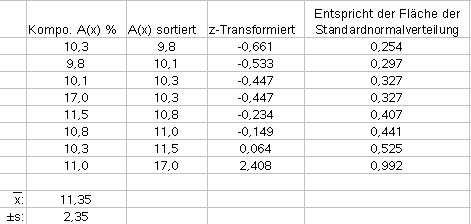
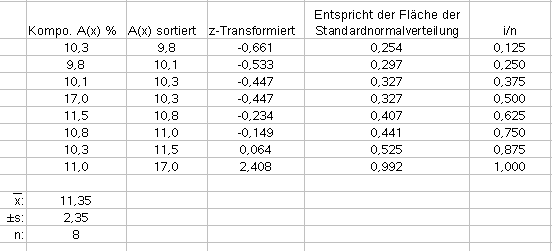
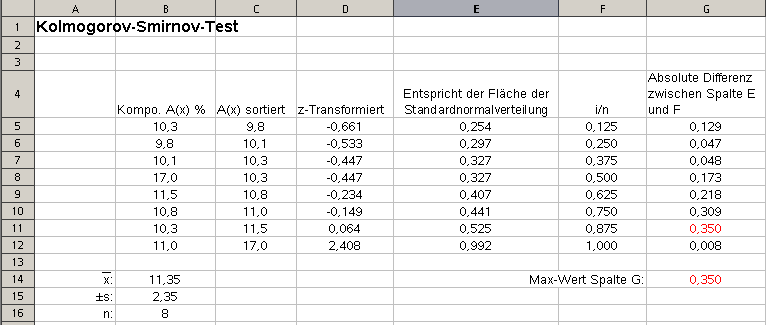
Kolmogorov-Smirnov-Test (Kolgoroff-Smirnoff-Test) Zur Durchführung des Chiquadrat-Tests zur Prüfung auf Normalverteilung müssen die Merkmalsausprägungen in Klassen eingeteilt werden.
Die Voraussetzung dazu ist, dass genügend Merkmalsausprägungen (Daten, Fallzahlen) vorliegen. Ist diese Voraussetzung nicht gegeben, also die Anzahl der Werte klein, wird als Anpassungstest auf Normalverteilung der Kolmogorov-Smirnov-Test herangezogen.
Bei einer kleinen Fallzahl ist eine signifikante Abweichung von der Normalverteilung (siehe auch Potenzmomente) selten zu beobachten, d. h., die Werte müssen ziemlich “auffällig” sein. Das Video KS-Test mit R beschreibt den Kommogov-Smirnov-Test zur Prüfung auf Normalverteilung mit der Statistikumgebung R
. An folgendem Beispiel wird der Test dargelegt. |