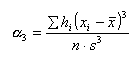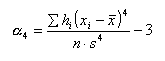Abweichung von der Normalverteilung


	*Zurück...*


	Zurück zum Lexikon Normalverteilung / Potenzmomente oder zur Seite Median.


	Abweichung von der Normalverteilung: Schiefe und Wölbung

Es werden 2 Typen möglicher Abweichungen von der Normalverteilung unterschieden:

1. Typ:
Die Verteilung ist unsymmetrisch oder schief, siehe rote Verteilung in der Grafik. Eine positive Schiefe, auch linkssteil genannt, liegt dann vor, wenn der Hauptanteil der Verteilung auf der linken Seite liegt.


	Es kann angenommen werden, das

	Linkssteile Verteilung: Modus < < Rechtssteile Verteilung: < < Modus.


	: Median : Mittelwert (Dichtemittel, Schwerpunkt)


	Der Mittelwert ist allerdings sehr empfindlich gegenüber Extremwerten (d. h. nicht robust), dadurch kann obige Annahme beeinflusst werden.

2. Typ:
Liegt das Maximum (Dichtemittel) bei gleicher Varianz höher als das einer Normalverteilung, also spitzer, liegt ein positiver Exzess und wenn das Maximum tiefer liegt, die Verteilung im Vergleich zur Normalverteilung abgeflacht ist, liegt ein negativer Exzess vor (siehe grüne Verteilung in der Grafik).

Die Schiefe (skewness) und Wölbung (kurtosis) wird über die Potenzmomente berechnet.

Potenzmomente

Abweichungen bezüglich der Schiefe von der Normalverteilung werden über den Momentkoeffizienten α₃geschätzt:

Für eine symmetrische Verteilung gilt α₃ = 0.
Ist α₃ positiv, liegt eine Linkssteile und ist α₃ negativ liegt eine rechtssteile Verteilung vor.

Abweichungen bezüglich der Wölbung von der Normalverteilung werden über den Momentkoeffizient α₄ geschätzt:

Für die Normalverteilung gilt α₄ = 0.
Ist α₄ positiv, liegt ein positiver Exzess, Hochgipfligkeit, vor. Ist α₄ hingegen negativ, liegt ein negativer Exzess, Flachgipfligkeit, vor.

Eine Schätzung bezüglich einer vermuteten Abweichung von der Normalverteilung kann auch über den Chi-Quadrat-Test (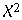-Test) erfolgen. Auf der Beispielseite sehen Sie auch ein Vergleich 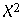-Test und Momentkoeffizienten α₃.

Unterstützung mit dem Statistikprogramm R

Möchten Sie die oben beschriebene Schätzungen nicht per Hand durchführen, kann Ihnen das freie Statistikprogramm R weiterhelfen! Wenn Ihnen R nicht geläufig ist, bietet Ihnen das Buch Einführung in R einen einfachen Einstieg.

Laden Sie die Funktion normalv() in die R-Arbeitsumgebung. x stellt die Daten als Vektor dar, die Sie auf Normalverteilung prüfen möchten. Der beispielhafte Aufruf der Funktion normalv() mit einem Vektor, bestehend aus 1000 simulierten Beobachtungen (Mittelwert = 1, Standardabweichung = 0,1), zeigt folgende Schätzung...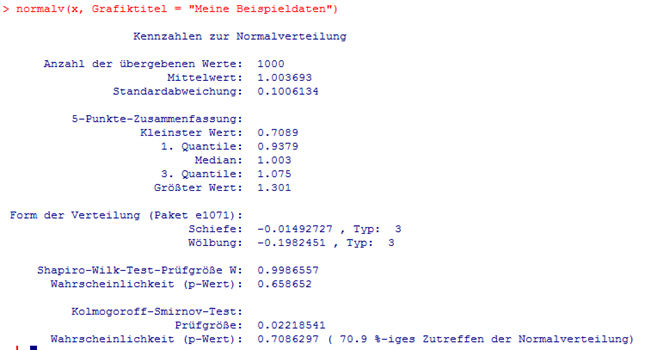

Funktion_normalv_V3

... und gibt folgende Grafiken aus:


	Hat der Inhalt Ihnen weitergeholfen und Sie möchten diese Seiten unterstützen?

Impressum

Datenschutz