Zeitreihenanalyse
Was ist eine Zeitreihe? Eine Zeitreihe entsteht, wenn zu einem Merkmal Y an aufeinander folgenden Zeitpunkten t (Zeitperiode t = 1,..., n) Beobachtungen yt durchgeführt werden. Diese zeitlich geordneten Beobachtungen yt des Merkmals Y bilden die Zeitreihe:
Eine Zeitreihe ist eine zeitlich geordnete Folge von Beobachtungen.
Das Ziel der Zeitreihenanalyse ist, Strukturen und Regelmäßigkeiten in Zeitreihen aufzudecken und zur Beschreibung oder Modellierung zu nutzen.
Bekannte Beispiele für Zeitreihen sind Aktienkurse (nur wenn online: OnVista.de ), Statistiken der Bundesanstalt für Arbeit (Arbeitslosenstatistik), der Preisindex bezüglich der Lebenshaltungskosten, Wetterdaten usw.. Sie führen sicher Ihre eigene Zeitreihe, wenn Sie an “Ihrer” Tankstelle vorbeifahren und die Preisentwicklung des benötigten Treibstofftypes beobachten.
Hier wird der Versuch unternommen, in die Zeitreihenanalyse einzuführen. Die Zeitreihenanalyse ist ein recht weites Gebiet und kann sich mathematisch aufwendig gestalten. Wenn Sie tiefer in die Thematik eindringen möchten, helfen die Literaturstellen Storm und Kreiß weiter. An dieser Stelle möchte ich die Verweise zur Stationarität und weißes Rauschen hervorheben.
Die Ausprägung des beobachteten Merkmals ist metrisch. Die Ausprägung kann aber durchaus ein Index sein, wie z. B. ein gewichteter Mittelwert oder eine qualitative Aussage wie”gut”, “befriedigend” oder “schlecht”, welche in einen Index transformiert wurde.
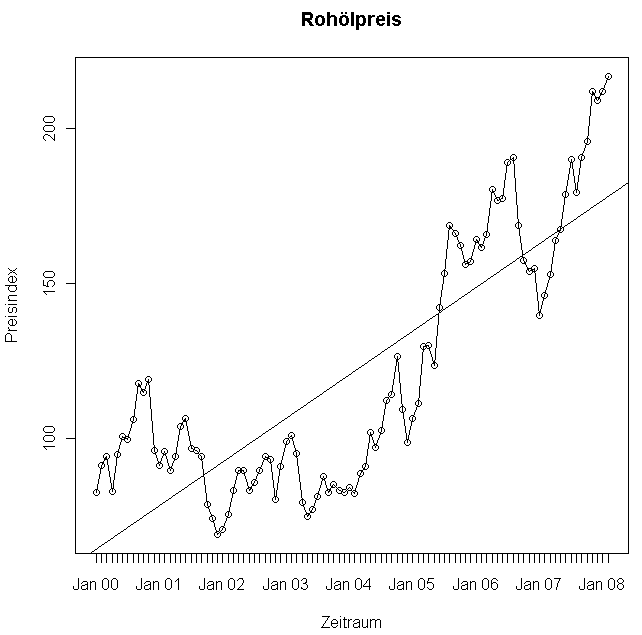
Betrachten wir als Zeitreihenbeispiel die Rohölpreisentwicklung (Abb.1):
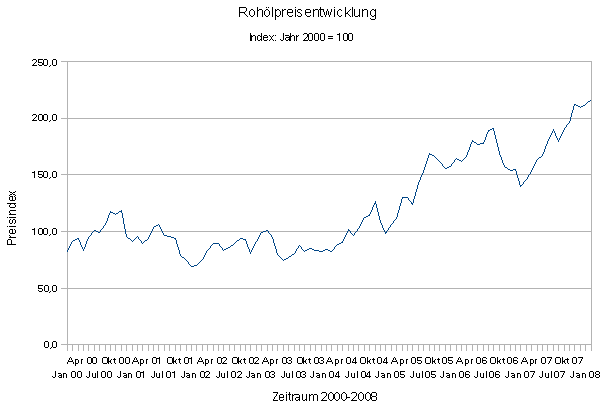
Abbildung 1: Rohölpreis
Quelle: Statistisches Bundesamt
In der Zeitreihenanalyse interessiert immer die Fragestellung, ob
- ein Trend als Funktion der Zeit, oder
- Saisoneffekte, z. B. jahreszeitliche Einflüsse, vorliegen.
Darüber hinaus wird der Versuch unternommen, auf Basis der vorliegenden Zeitreihe
- Prognosen über den zukünftigen Verlauf
zu erstellen. Auch die Frage der
- Korrelation, der Abhängigkeit zeitlich unterschiedlicher Beobachtungen,
ist von Bedeutung.
Eine Zeitreihe besteht aus Komponenten (Komponentenmodell), der systematischen und irregulären (Rest-)Komponente. Die systematischen Komponenten sind Trend, Saison und weitere erklärbare Effekte.
Zu der Restkomponente werden nicht erklärbare oder erfassbare Einflüsse zusammengefasst (siehe Regressionsanalyse Residuen). Um die Komponenten zu zerlegen (sie werden ja gemeinsam beobachtet) werden Modelle angenommen, die nachfolgend behandelt werden.
Das additive Komponentenmodell
Für dieses Modell wird angenommen, dass sich die Komponenten k additiv verhalten:
yt = k1t + k2t + ... + et t = 1, ..., n
k1: Trendkomponente
k2: Saisonkomponente
et: Restkomponente
...: weitere einflussnehmende Komponenten, z. B. aus dem wirtschaftlichen Bereich die Konjunkturkomponente
Die Trendkomponente k1 (oder auch m) steht für systematische Veränderungen, etwa ein lineares oder exponentielles Wachstum. Die Saisonkomponente k2 (oder s) beinhaltet saisonal wiederkehrende Veränderungen. Als Beispiel sei hier die jahreszeitlichen Veränderungen in der Arbeitslosenstatistik für das Baugewerbe in den Wintermonaten genannt. Wenn wir nun schon bei der Arbeitslosenstatistik sind, kann die ...-Komponente durchaus die Konjunkturkomponente sein.
Lassen sich Komponenten im Modell nicht exakt trennen (also getrennt beschreiben), werden diese zur glatten Komponente g zusammengefasst. Dadurch wird das additive Modell vereinfacht zum Trend-Saison-Modell:
yt = gt + st + et t = 1, ..., n
Neben dem additiven Modell findet das multiplikative Modell Anwendung:
yt = gt * st * et t = 1, ..., n
Bei diesen Modellen besteht eine Ähnlichkeit zu Regressionsmodellen. Es ist aber zu beachten, das Trend und Saison unbeobachtbare Funktionen sind, die über die Zeitreihenanalyse geschätzt werden. Zur Schätzung dieser Komponenten wird von einem globalen oder lokalem Ansatz ausgegangen.
Globaler Ansatz
Globale Trendmodelle sind (sollen) über den gesamten beobachteten Zeitbereich gültig (sein). Globale Modelle sind dadurch starrer als die später dargelegten lokale Modelle.
Der einfachere Fall des globalen Ansatz ist das reine Trendmodell
yt = gt + et
da es sich auf das Schätzen der Trendkomponente gt reduziert. Diese Schätzung erfolgt über die Regressionsanalyse und die lineare Trendfunktion
gt = a0 + a1t + et
ist Ihnen sicher geläufig. Wie auch im Bereich der Regressionsanalyse beschrieben, kommen auch Funktionen, wie quadratische, exponentielle usw. als Trendfunktion in Frage. Bei polynomialen Modellen höherer Ordnung ist zu berücksichtigen, dass sie außerhalb des Datenbereiches instabil sind und deswegen für Prognosezwecke ungeeignet sein können.
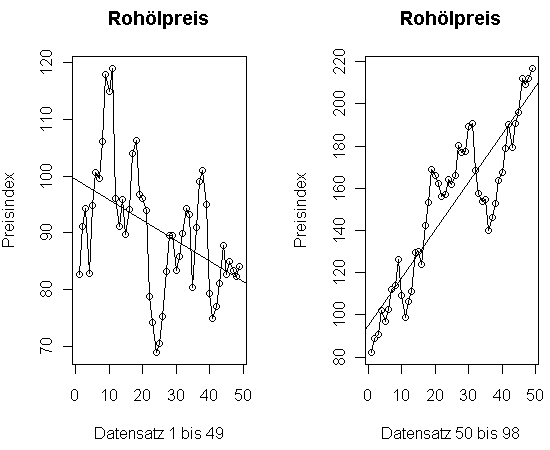
In Abbildung 2 wird, trotz des spekulativen Anteils, von einem linearen Trend ausgegangen und die Regressionsgerade eingezeichnet: