 |
Clusteranalyse | |||||||||||
Über die Clusteranalyse werden Gruppen innerhalb Beobachtungen identifiziert. Die Clusteranalyse steht damit methodisch vor der Varianz- und der Diskriminanzanalyse, da bei diesen Verfahren eine Gruppeneinteilung vorausgesetzt wird. Schauen Sie sich auch das Video Clusteranalyse mit R zur Einführung an. Der Begriff Clusteranalyse steht für unterschiedliche Verfahren zur Gruppenidentifizierung anhand der Eigenschaften der beobachteten Objekte. Über diese Eigenschaften werden Verwandtschaften über Distanz- oder Ähnlichkeitsmaße mit den Verfahren der Clusteranalyse ermittelt. Die dann ermittelten Gruppen sollen praktisch keine Ähnlichkeit besitzen. Die Clusteranalyse beurteilt zur Gruppenbildung (Clusterbildung) alle Eigenschaften der beobachteten Objekte (polythetisches Verfahren) und ist ein strukturentdeckendes Verfahren. Der Ablauf einer Clusteranalyse findet prinzipiell über 2 Schritte statt (Abb. 1): | |||||||||||
 | |||||||||||
Abbildung 1 | |||||||||||
Die Bestimmung der Ähnlichkeit, des Proximitätsmaßes, erfolgt ebenso wie die Bestimmung der Clusteranzahl über verschiedene Verfahren und wird auf der Seite der Distanzbestimmung ausführlich dargelegt. |
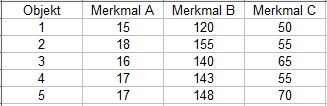 | ||
Abb. 2 | ||
Die euklidische Distanzmatrix der Abbildung 2 zeigt Abbildung 3 und sie ist die Ausgangsbasis zur Clusteranalyse: |
|
| ||||||||||||||||||||
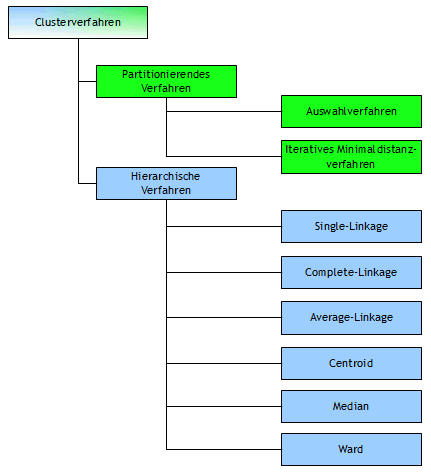 | ||
Abbildung 4 | ||
|
| ||||||||||||||||||||||||||||||||||||||||
Die Distanzbildung zwischen dem neuen Cluster (X+Y) und zwischen irgendeiner Gruppe R (oder einem Objekt) der reduzierten Distanzmatrix wird nach F1 gebildet: |
D(R, X+Y) = A*D(R,X)+B*D(R,Y)+E*D(X,Y)+G*abs[D(R,X)-D(R,Y)] | |||
F1 | |||
A, B, E und G sind Konstanten, die vom Verfahren abhängig sind | |||
Tabelle 1 zeigt die Konstanten zum agglomerativen Verfahren: |
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Tabelle 1 |
Im Single-Linkage-Verfahren werden im 1. Schritt die beiden Objekte X und Y vereinigt, die die kleinste Distanz aufweisen. Im Beispiel Abbildung 3 sind das die Objekte X = 5 und Y = 3 mit D(X,Y) = 9,69. Das Objekt D(5,3) stellt nun eine Gruppe (Startpartition) dar. Die Distanz dieser Gruppe wird als Folgeschritt zu den übrigen Objekten R der Gruppe nach F2 (Single Linkage) gebildet: D(R, X+Y) = 0,5*[D(R,X)+D(R,Y)-abs[D(R,X)-D(R,Y)] |
F2 |
Die Objekte der reduzierten Matrix R sind die Objekte 1, 2 und 4. Die neue Distanzmatrix wird nach dem Schema in Abbildung 5 über F2 wie folgt gebildet: |
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Durch die ermittelten Distanzen des Objektes D(X,Y) zu den verbleibenden Objekten 1, 2 und 4 erhalten wir, nach Eleminierung der Zeilen und Spalten der fussionierten Objekte D(X,Y) aus der Matrix Abbildung 3, die neue reduzierte Distanzmatrix (Abb. 9): |
|
Abb. 9 |
Führen wir nach Abb. 5 einen weiteren Durchlauf durch! Dazu wird das Objekt 4 (kleinste Distanz) zur Gruppe Objekt 5+3 addiert. Die Distanz zu den verbleibenden Objekten 1 und 2 wird wieder nach F2 berechnet: |
|
| ||||||||||||||||||||||||||||||||||||||||||||
Als Resultat erhalten wir eine neue Distanzmatrix zwischen dem Objekt (5+3+4) und den Objekten 1 und 2 (Abbildung 12): |
|
Abb. 12 |
Die gebildeten Cluster unterliegen Ihrer Interpretation, d. h., ist eine weitere Gruppenbildung sinnvoll oder nicht? Die Gruppenbildung ist ebenso von der Relevanz der betrachteten Objekteigenschaften abhängig. Eingangs wurde als Vorteil der Clusteranalyse genannt, dass alle Objekteigenschaften zur Clusteranalyse herangezogen werden können. Empfehlenswert ist es allerdings, diese bezüglich ihrer Relevanz zu beurteilen. Konstante Objekteigenschaften sollten nicht in die Clusteranalyse einbezogen werden! Wir nehmen uns die Interpretationsfreiheit und beenden die Clusteranalyse für dieses Beispiel mit dem Vorliegen der 3 Clustern Objekt (5+3+4), Objekt 1 und Objekt 2. Das Statistikprogramm R bietet über die Funktion hclust() und deren Methode single (Single-Linkage) eine einfache Möglichkeit der Clusteranalyse. Abbildung 13 zeigt das Ergebnis der Distanzmatrix aus Abbildung 3 über die Funktion hclust(), das mit unserer manuellen Rechnung übereinstimmt: |
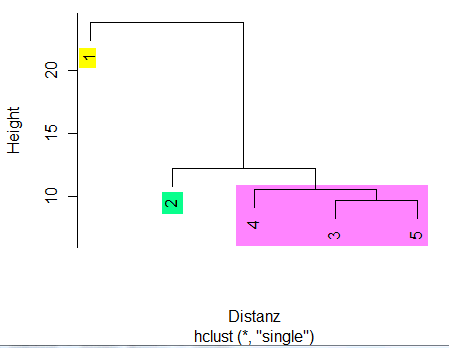 | |
Abb. 13 | |
Die R-Funktion hclust() bietet auch die in Abbildung 4 unter den hierarchischen Verfahren gezeigten Methoden an. Auf das Ward-Verfahren wird hier nicht eingegangen, sondern nur erwähnt, dass dieses Verfahren in der Praxis eine weite Verbreitung gefunden hat. Erwähnen möchte ich neben hclust() die Funktion agnes() aus dem Paket cluster und die agglomerativen Verfahren Single-, Complete- und Average-Linkage darstellen: Die Daten zur Cluster-Analyse zeigen bezüglich der Größe zwischen den Merkmalen A, B und C deutliche Unterschiede (siehe Abb2). Besonders zwischen den Merkmalen A und B liegt fast eine 10er-Potenz! Derart große Differenzen zwischen den Merkmalen können die Aussagen zur Clusterbildung negativ beeinflussen und deswegen werden die Daten mit stand=T standardisiert. Fehlende Werte (Beobachtungen) müssen ebenfalls aus den Daten zur Clusteranalyse entfernt werden! Aber fangen wir an...! > Cluster_Daten Single-Linkage-Verfahren: > Single_Verfahren <- agnes(Cluster_Daten, stand=T, method = "single")
Height zeigt die Heterogenität der gebildeten Cluster an und demnach ist der Unterschied zu z. B. 3 & 4 sehr deutlich! Auf welcher Höhe die Cluster verschmolzen wurden, kann auch als Zahlenwert ausgegeben werden: > sort(Single_Verfahren$height) D. h., die Objekte 3 & 4 wurden auf der Höhe 2.064 verschmolzen und das Objekt 1 auf der Höhe 3,73. Der agglomerative Koeffizient (AC) liegt zwischen 0 und 1, sollte als Resultat einer guten Clusterschätzung über 0,5 liegen. Nebenbei bemerkt, die Clusterbildung entspricht der Funktion hclust(). Compelte-Linkage-Verfahren: > Complete_Verfahren <- agnes(Cluster_Daten, stand=T, method = "complete") Die beiden Verfahren Single- und Complete-Linkage unterscheiden sich deutlich in der Höhe der Clusterbildung und dem AC-Koeffizienten. Average-Linkage-Verfahren: > Average_Verfahren <- agnes(Cluster_Daten, stand=T, method = "average") Beurteilen Sie die Güte der Verfahren selber! Die Differenz zwischen Complete und Average ist nicht besonders deutlich! |
Hat der Inhalt Ihnen weitergeholfen und Sie möchten diese Seiten unterstützen? |