 |
Distanz und Ähnlichkeit | ||
| |||||||||||||||||||||||||||||||||||||
Tabelle 1 |
Über die Objektmerkmale wird das Proximitätsmaß ermittelt, um darüber eine Aussage bezüglich der Distanz oder Ähnlichkeit der Objekte machen zu können. Dabei gilt:
Abhängig vom Skalenniveau der Merkmale, kommen unterschiedliche Proximitätsmaße zur Anwendung (Abb. 1): |
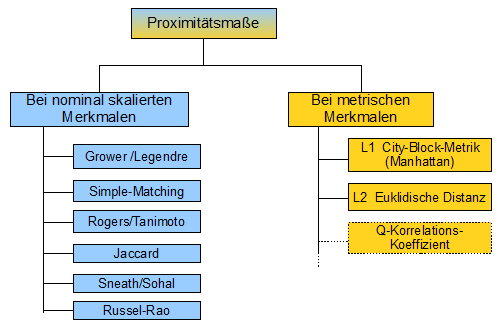 | |||
Abbildung 1 | |||
Proximitätsmaße für metrische Merkmale Für metrische Merkmale berechnen wir die Distanz auf Basis des folgenden Beispiels (Tabelle 2): |
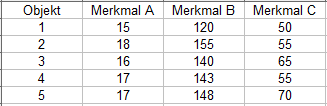 | |||
Tabelle 2 | |||
Die Distanz dij zwischen zwei Objekten ist der kürzeste Abstand der zum Objekt gehörigen Merkmalausprägungen, dargestellt als Punkte in Abb. 2. |
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Durch diesen gedanklichen Sprung, ist es möglich, diese Methodik auch auf Punkte im höherdimensionierten Raum zu übertragen: |
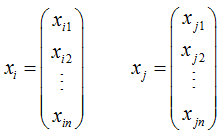 | |||||||||||
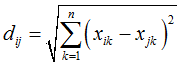 | |||||||||||
F2 | |||||||||||
Die euklidische Distanz wird auch L2-Norm genannt (siehe Abb. 1) und ist eine Variante der sogenannten Minkowski-Metrik (F3): | |||||||||||
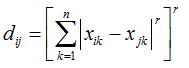 | |||||||||||
F3 | |||||||||||
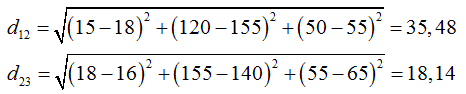 |
Um die gesamte Distanz-Matrix zu berechnen, bemühen wir das freie Statistikprogramm R. Die Distanz-Matrix wird über die Funktion dist() berechnet. Die Matrix hat die Dimension m*m, wobei m der Objektanzahl entspricht. Für das Beispiel aus Tabelle 2 wird eine 5 * 5-Matrix erwartet (Abb. 3). |
|
| ||||||||||||||||||||
Die Objekte 3 und 5 (d53) sind sich am ähnlichsten, weil die Distanz zwischen diesen Objekten mit d53 = 9,49 am geringsten ist. Eine Ähnlichkeit zwischen dem 3. und 4. Objekt ist mit d43 = 10,49 ebenfalls nicht von der Hand zu weisen. Die Hauptdiagonale ist immer 0, da natürlich z. B. das Objekt 1 zu sich selbst eine 100 %ige Ähnlichkeit besitzt. Die Merkmalausprägungen der Objekte unterliegt Streuungen. Dadurch kann die Distanz dij zwischen den Objekten durch die Merkmale dominiert werden, die eine entsprechend große Streuung besitzen. Dieser Umstand ist besonders zu berücksichtigen, wenn zwischen den Objektmerkmalen, wie in unserem Beispiel (Tabelle 2), deutliche Größenunterschiede bestehen. Um die Streuung zu berücksichtigen, werden die Merkmale skaliert. Wird die Distanz über die L2-Norm bestimmt, kann die Skalierung über die Standardabweichung s durchgeführt werden. Dazu wird F2 um die quadratische Standardabweichung s ergänzt (F3)... |
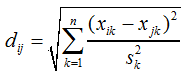 | |||||
F3 | |||||
... und Tabelle 2 wird um die Standardabweichungen s erweitert (Tabelle 3): | |||||
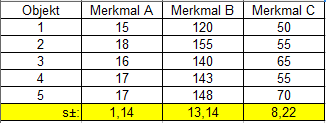 | |||||
Tabelle 3 | |||||
Mit der Standardabweichung s der Objektmerkmale aus Tabelle 3 lässt sich nun über F3 die skalierte Distanz berechnen (Tabelle 4): |
|
Tabelle 4 |
Nach der Skalierung über die Standardabweichung wird die Ähnlichkeit zwischen den Objekten 3 und 5 bestätigt. Anstelle der Ähnlichkeit zwischen dem 3. und 4. Objekt der unskalierten Distanz, drängt sich nach der Skalierung eine hohe Ähnlichkeit zwischen dem 2. und 4. Objekt auf. Neben dem oben dargelegten Einfluss der Merkmalvarianz müssen Sie sich bewusst sein, dass die Ähnlichkeit von der Methode abhängt! Abbildung 4 zeigt die Distanzmatrizen der Daten aus Tabelle 2 einmal nach der schon dargelegten euklidischen Methode (L2-Norm) und nach der Manhattan- Methode (L1-Norm). Der jeweils kleinste Distanzwert ist farblich markiert. |
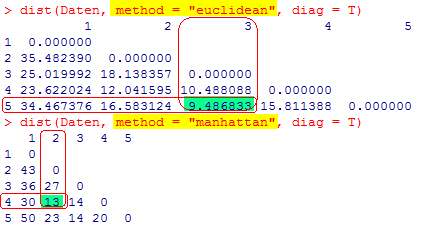 | ||||
Abbildung 4 | ||||
Proximitätsmaße für nominale Merkmale | ||||
Nominale Merkmale, die mehr als zwei
Merkmalausprägungen aufweisen, werden zur Ermittlung der Ähnlichkeit in binäre Hilfsvariablen zerlegt. Diese binären Hilfsvariablen nehmen dann in Abhängigkeit der Merkmalausprägung den Wert 1, wenn die Eigenschaft vorliegt oder den Wert 0, wenn die Eigenschaft nicht vorliegt, an. Im binären Merkmalvergleich zweier Objekte, lassen sich beim Vergleich folgende Fälle unterscheiden:
|
| |||||||||||||||||||||||
Tabelle 5 |
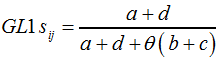 | ||||||||
F4 | ||||||||
Der Parameter | ||||||||
|
F5 | ||||||||
Nimmt der Parameter |
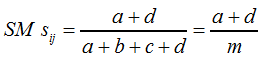 | |||
F6 | |||
... und das Distanzmaß SM dij nach F7: |
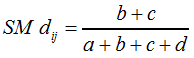 | ||
F7 | ||
Beispiel für den Simple-Matching-Koeffizient SM sij: |
|
Tabelle 6, binäre Beispielmatrix |
Die Tabellen 7 und 8 zeigen die Fallunterscheidungen nach Tabelle 5 für die Tabelle 6. In Tabelle 7 bedeutet “Symmetrieannahme” dass das Vorhandensein gleicher Eigenschaften für Merkmal A und das Nichtvorhandensein gleicher Eigenschaft für Merkmal D jeweils zu einem Eintrag ins a-Feld, also 1 + 1, führt. |
|
| ||||||||||||||||||||||||||||
Der Simple-Matching-Koeffizient SM sij nach F6 nimmt für Tabelle 7 folgendes Ähnlichkeitsmaß an (F8) ... |
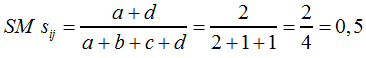 | |||||||
F8 | |||||||
... und für Tabelle 8 nimmt der Koeffizient folgenden Wert (F9) an: | |||||||
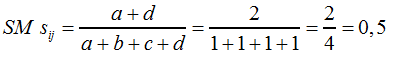 | |||||||
F9 | |||||||
Nimmt der Parameter |
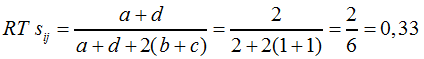 | ||||||||||||||||||||||||
F10 |
||||||||||||||||||||||||
Die dazugehörige Distanz RT dij wird über F11 berechnet: | ||||||||||||||||||||||||
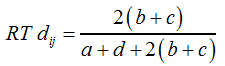 | ||||||||||||||||||||||||
F11 | ||||||||||||||||||||||||
Eine Variante des GL1-Koeffizienten ist der GL2-Koeffizient nach F12 ... | ||||||||||||||||||||||||
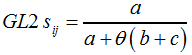 | ||||||||||||||||||||||||
F12 | ||||||||||||||||||||||||
... mit | ||||||||||||||||||||||||
F13 | ||||||||||||||||||||||||
Den Jaccard-Koeffizienten als Ähnlichkeitsmaß erhalten wir, wenn in F12 der Parameter | ||||||||||||||||||||||||
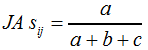 | ||||||||||||||||||||||||
F14 | ||||||||||||||||||||||||
... und die dazugehörige Distanz JA dij nach F15: | ||||||||||||||||||||||||
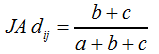 | ||||||||||||||||||||||||
F15 | ||||||||||||||||||||||||
Wird in F12 der Parameter | ||||||||||||||||||||||||
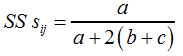 | ||||||||||||||||||||||||
F16 | ||||||||||||||||||||||||
... und die Distanz SS dij nach F17: |
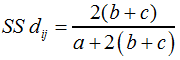 | ||||||
F17 | ||||||
Die sicher nicht vollständige Aufzählung wird mit dem Russel-Rao-Koeffizienten, der über F18 bestimmt wird, abgeschlossen: | ||||||
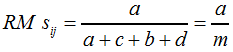 | ||||||
F18 | ||||||
Die oben erwähnte R -Funktion dist() berechnet für die in Abb. 5 dargestellte binäre Objektmatrix die ebenfalls in Abb. 5 dargestellte symmetrische Jaccard-Distanz-Matrix: |
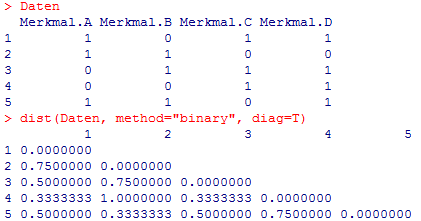 | |||||
Abbildung 5 | |||||
Hat der Inhalt Ihnen weitergeholfen und Sie möchten diese Seiten unterstützen? |