 |
Vektoren und deren Rechenoperationen |
|
| ||||||||||||||||||||||||||||||||||||||||||||
Ein Vektor im 3-dimensionalen Raum wird dann natürlich wie folgt dargestellt: |
Oben wurde dargelegt, dass ein Ortsvektor durch seine |
|
beschrieben wird. |
|
|
Die Vektoren |
Der Ortsvektor |
Praktisch bedeutet dies, dass alle möglichen parallelen Vektoren des Beispiels (siehe Bild 3) mit Rechnen mit Vektoren |
Addition: Vektoren, z. B. |
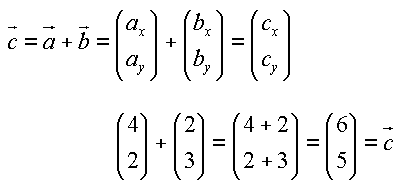 |
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Subtraktion: Die Gegenoperation zur Addition ist die Subtraktion: |
|
| ||||||||||||||||
Skalare Multiplikation: In der skalaren Multiplikation eines Vektors wird jedes Element des Vektors mit dem Skalar (der Zahl) multipliziert: |
Allgemein: | ||||
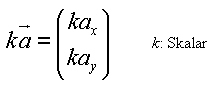 | ||||
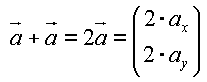 | ||||
|
| ||||||||||||||||
Linearkombination Wird der Vektor |
Der/die Vektor(en) |
Nullvektor und lineare Abhängigkeit Der Nullvektor wird, basieren auf dem Beispiel der Linearkombination, über |
erreicht. |
Der Vektor | |||||
wird von linearer Unabhängigkeit gesprochen. Skalares Produkt zweier Vektoren Das skalare Produkt zweier Vektoren ist die Summe der Produkte der gleichstelligen Koordinaten: |
|
|
Es spielt keine Rolle, ob Vektoren Zeilen- oder Spaltenvektoren sind. |
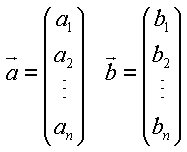 | ||
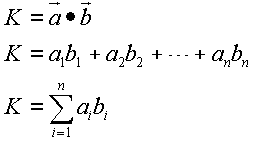 | ||
Ist das Skalarprodukt zweier Vektoren = 0, dann sind die Vektoren orthogonal (normal) zueinander. Skalares Produkt und Winkelfunktionen Wie lässt sich der Winkel |
|
|
Dazu denken wir uns ein rechtwinkliges Dreieck in obiger Abbildung (Bild 7), ermitteln den Projektionsvektor b’... |
|
|
... und können folgenden Zusammenhang erkennen: |
|
|
Wie wird der Betrag des Vektors |
|
| |||||||||||||||||||||||||||||
Der Betrag für einen Vektor im n-dimensionalen Raum wird ebenso berechnet: |
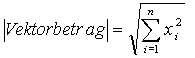 | ||||||
Die erste Hürde zur Berechnung des Winkels | ||||||
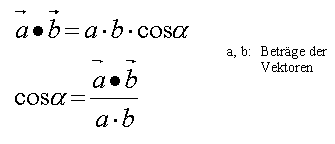 | ||||||
Kommen wir wieder zurück zu dem Eingangs genannten Beispiel in Bild 6. Für dieses Beispiel wird der Winkel | ||||||
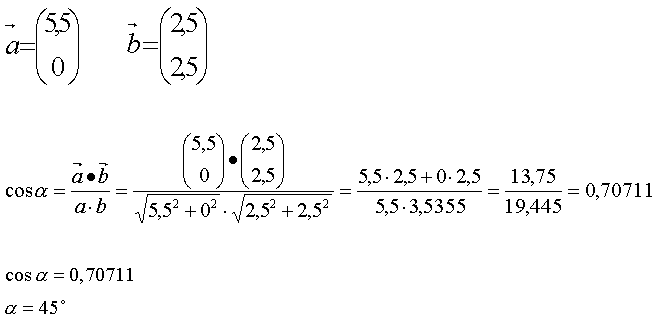 |
Der Winkel |
Hat der Inhalt Ihnen weitergeholfen und Sie möchten diese Seiten unterstützen? |