Zurück...

Lorenzkurve

Mit der Lornzkurve lassen sich Merkmale bezüglich ihrer Konzentrationverteilung, z. B. die Umsätze (Marktanteile) mehrerer Unternehmen (Merkmale) bezogen auf einen Markt, darstellen.

Dazu werden nur positive kardinalskalierte Merkmalsausprägungen (-werte) betrachtet.

Die Merkmale, die zur Darstellung als Lorenzkurve herangezogen werden sollen, werden der Größe nach aufsteigend sortiert, x₁ <= ... <= x_n, und die Punkte der Lorenzkurve ergeben sich über

Liegt der Idealfall vor, wobei dieser sicher vom Standpunkt abhängt, also bei einer “Konzentrationsgleichverteilung”, sieht die Lorenzkurve wie folgt aus:

Liegt eine Abweichung von der Gleichverteilung vor, d. h., um beim Umsatzbeispiel zu bleiben, gibt es unter den Unternehmen einen “Umsatzriesen”, weicht die Lorenzkurve wie im nächsten Bild von der Ideallinie (45°) ab:

Im folgenden wird ein Beispiel, in dem es um 5 Unternehmen geht, die ihren Umsatz in z. B. Hamburg erwirtschaften, gezeigt.

Danach wird der Anteil Merkmalsträger u und die kumulierte relative Merkmalssumme v berechnet....

... und graphisch dargestellt:

Im obigen Beispiel wird graphisch die starke Konzentrationsverschiebung auf das Unternehmen 2 gezeigt. Dieses Unternehmen hat den größten Marktanteil.
Die Grafik zeigt Ihnen nun optisch die Konzentrationsverschiebung an, aber mit Hilfe des Gini-Koeffizienten kann diese auch zahlenmäßig ausgedrückt werden.

Gini-Koeffizient

Die Stärke der Konzentration, also die Abweichung von der Gleichverteilung, drückt sich durch die Entfernung von der 45°-Linie aus.
Der Gini-Koeffizient G ist das Verhältnis aus der Fläche zwischen der 45°-Linie (Diagonale) und Lorenzkurve und der Gesamtfläche (= Fläche zwischen Diagonale und u-Achse):

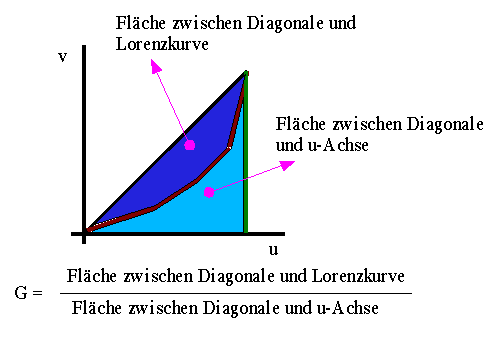Da der Gini-Koeffizient nur im Zusammenhang mit der Lorenzkurve zu betrachten ist, gelten hier die gleichen Voraussetzungen für die Merkmalsausprägungen.

Der Gini-Koeffizient wird wie folgt berechnet:

Berechnung des G-Koeffizienten auf Basis des obigen Beispiels:

Der Gini-Koeffizient beträgt bei Gleichverteilung 0 und bei maximaler Konzentration (n-1)/n:

Aus G_max ist ersichtlich, dass die maximale Ausprägung des Koeffizienten von der Merkmalsanzahl abhängt. Um diese Abhängigkeit zu vermeiden, wird der G-Koeffizient normiert:

Der G-Koeffizient ist immer mit der Lorenzkurve zu betrachten.

Obige Beispiele können mit den Standardfunktionen des Tabellenprogramms von OpenOffice  berechnet werden. Verwenden Sie das Statistikprogramm R können Sie die Funktion Lorenz downloaden.

Hat der Inhalt Ihnen weitergeholfen und Sie möchten diese Seiten unterstützen?