
 |
Die Binomialverteilung ist eine diskrete Wahrscheinlichkeitsverteilung für ein Merkmal, das z. B. aus zwei Ausprägungen, z. B. funktionsfähig/defekt, Wappen oder Zahl, oder blau/rot mit einer konstanten Erfolgswahrscheinlichkeit p für eine Ausprägung, z. B. defekt oder rot, annehmen kann. |
|
| ||||||||||||||||
n: Stichprobenumfang |
Voraussetzungen zur Anwendung der Binomialverteilung: |
| ||||||||||||||||||||||||||||||||
Beispiel: | ||||||||||||||||||||||||||||||||
Eine Glühbirnenfertigung läuft mit einem konstanten Ausschußanteil von 5% (p = 0,05). Zur Qualitätsprüfung werden 5 Leuchtkörper (Stichprobenumfang n = 5) entnommen. Im Folgenden werden die Wahrscheinlichkeiten P für das Vorfinden von genau 0, 1, 2, 3, 4 und 5 defekte Glühbirnen berechnet: | ||||||||||||||||||||||||||||||||
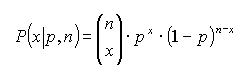 | ||||||||||||||||||||||||||||||||
a) P(genau 0): | ||||||||||||||||||||||||||||||||
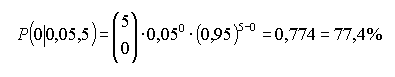 | ||||||||||||||||||||||||||||||||
b) P(genau 1): | ||||||||||||||||||||||||||||||||
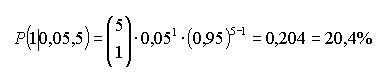 | ||||||||||||||||||||||||||||||||
c) P(genau 2): | ||||||||||||||||||||||||||||||||
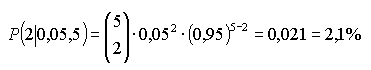 | ||||||||||||||||||||||||||||||||
d) P(genau 3): | ||||||||||||||||||||||||||||||||
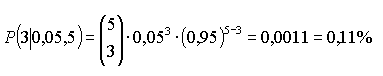 | ||||||||||||||||||||||||||||||||
e) P(genau 4): | ||||||||||||||||||||||||||||||||
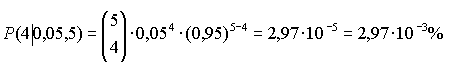 | ||||||||||||||||||||||||||||||||
f) P(genau 5): | ||||||||||||||||||||||||||||||||
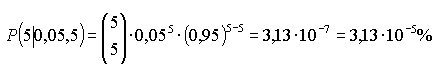 | ||||||||||||||||||||||||||||||||
Obiges Beispiel macht deutlich, wie sicher auch vermutet, z. B. genau 3 defekte Glühbirnen in dem Stichprobenumfang n = 5 Stück vorzufinden, sehr gering ist (P = 0,1%). Lautet die Fragestellung “Wie hoch ist die Wahrscheinlichkeit P höchstens 2 defekte Leuchtkörper in dem Stichprobenumfang n vorzufinden?” muss über die Wahrscheinlichkeitssumme PSum (siehe Wahrscheinlichkeit, Oder-Regel) gegangen werden: | ||||||||||||||||||||||||||||||||
P(höchstens x) = P(0) + P(1) + P(2) + ... + P(x) P(höchstens 2) = 0,774 + 0,204 + 0,021 = 0,999 | ||||||||||||||||||||||||||||||||
Lautet sie hingegen “Wie hoch ist die Wahrscheinlichkeit P mindestens 2 defekte Leuchkörper im Stichprobenumfang n vorzufinden?”, wird sie wie folgt beantwortet: | ||||||||||||||||||||||||||||||||
P(mindestens x) = 1- P(höchstens x-1) P(mindestens 2) = 1- (0,774 + 0,204) = 0,022 | ||||||||||||||||||||||||||||||||
Hat der Inhalt Ihnen weitergeholfen und Sie möchten diese Seiten unterstützen? | ||||||||||||||||||||||||||||||||