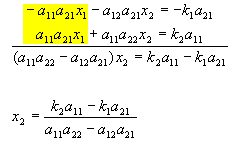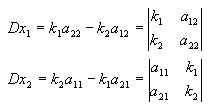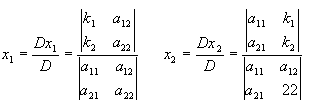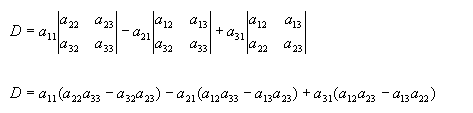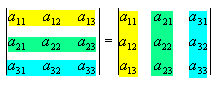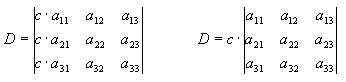Determinanten (determinare (lat.) = bestimmen) gehören zum Gebiet der linearen Algebra mit beliebig vielen Unbekannten (Matrizenrechnung).
Sie liefern Kriterien darüber, ob ein Gleichungsystem eine eindeutige Lösung hat und ist ein mathematisches Hilfsmittel, um die Lösung eines linearen Gleichungssystems mit einem Mindestmaß an Rechenarbeit zu erhalten.
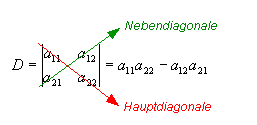
Einleitend wird die Determinante an einem System von zwei Gleichungen 1. Grades (die Unbekannten liegen nicht potenziert vor) mit zwei Unbekannten dargelegt:
- a11x1 + a12x2 = k1
- a21x1 + a22x2 = k2
Wie Sie sich sicher erinnern können, kann das Additionsverfahren zur Lösung angewendet werden: Additionsverfahren zur Erinnerung: Im Additionsverfahren werden die Gleichungen durch Multiplikation mit geeigneten Zahlen so umgeformt,
dass bei der Addition der neuen Gleichung eine Unbekannte wegfällt. Dadurch wird eine Gleichung mit einer Unbekannten erhalten.
Die zweite Unbekannte wird dadurch bestimmt, indem der für die erste Unbekannte ermittelte Wert in eine der Gleichungen eingesetzt und dann aufgelöst wird. Für x1: Multiplikation mit a22 und -a12: - a11x1 + a12x2 = k1 * a22
- a21x1 + a22x2 = k2 * -a12
Durchgeführter Multiplikationsschritt: - a11a22x1 + a12a22x2 = k1a22
- -a12a21x1 - a12a22x2 = -k2a12
(Die folgenden Gleichungen sind zur besseren Darstellung garfisch dargestellt!)
|